Chapter 8: Long Call Butterfly

Abhinav’s manager gets a transfer to another department. Abhinav now reports to a new manager, Simran. Her market outlook for the near future for a stock PQR Ltd. is neutral. She believes that the market will be neither bullish nor bearish. She asks Abhinav to come up with Options strategies for PQR Ltd.

Abhinav initially suggests two multi-leg Options: A Long Call Butterfly and a Short Straddle. Let’s take a look at the Long Call Butterfly in this chapter. 

Long Call Butterfly

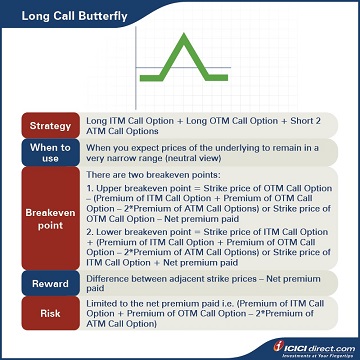
A Long Call Butterfly strategy involves selling two At-the-Money (ATM) Call Options and simultaneously purchasing one In-the-Money (ITM) Call Option and one Out-of-the-Money (OTM) Call Option. Here, the three strike prices have an equal difference.

This three-part strategy is used for a neutral view of the market, that is, when the trader expects the prices of the underlying to remain in a very narrow range or expects minimum volatility. By entering into a Long Call Butterfly Option for PQR Ltd., Abhinav can capture this low volatility at a nominal cost by buying and selling an equal number of Options.

• The maximum risk in this strategy is limited to the extent of the initial cost of the net premium paid.
• The maximum profit is incurred when the spot price equals the strike prices of ATM Call Options.

Strategy: Long 1 x ITM Call Option (Leg 1) + Long 1 x OTM Call Option (Leg 2) + Short 2 x ATM Call options (Leg 3)

When to use: When you expect prices of the underlying to remain in a very narrow range (neutral view)

Breakeven: Since there are three trades involved, there are two breakeven points:

1. Upper breakeven point = Strike price of OTM Call Option – (Premium of ITM Call Option + Premium of OTM Call Option – Premium of ATM Call Options) or Strike price of OTM Call Option – Net premium paid

2. Lower breakeven point = Strike price of ITM Call Option + (Premium of ITM Call Option + Premium of OTM Call Option –      Premium of ATM Call Options) or Strike price of ITM Call Option + Net premium paid

Maximum profit: Difference between adjacent strike prices – Net premium paid

Maximum risk: Limited to the net premium paid i.e. (Premium of ITM Call Option + Premium of OTM Call Option – 2*Premium of ATM Call Option)

Let’s understand the Long Call Butterfly strategy with an example:

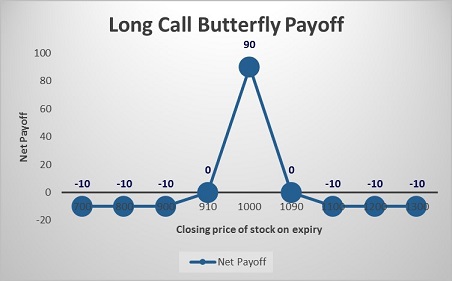
Let’s assume that the spot price of PQR Ltd. is Rs. 1,000. Simran has a neutral view of this stock. Abhinav suggests buying one ITM Call of strike price Rs. 900 at Rs. 140, and also buying one OTM Call of strike price Rs. 1,100 at Rs. 30. He also suggests selling two ATM Call Options of strike price Rs.1000 at Rs. 80. He would have paid a total premium of Rs. 140 + Rs. 30 – 2* Rs. 80 = Rs. 10, and this will be the maximum loss. He will make maximum gains when the stock doesn’t move.

Let’s look at the cash flow in various scenarios:

Let’s understand the payoff in various scenarios. It will give you a fair idea of how we have arrived at the above values.

If the stock closes at Rs. 800 on expiry: All the three legs expire OTM

Leg 1: Premium paid on the ITM Call Option of strike price Rs. 900 = Rs. 140

Premium received on ITM Call Option of strike price Rs. 900 at expiry = Max {0, (spot price – strike price)} = Max {0, (800 – 900)} = Max (0, – 100) = 0

So, payoff from the ITM Call Option = Premium received – Premium paid = 0 – 140 = – Rs. 140

Leg 2: Premium paid on the OTM Call Option of strike price Rs 1100 = Rs. 30

Premium received on an OTM Call Option of strike price Rs. 1100 at expiry = Max {0, (Spot price– Strike price)} = Max {0, (800 – 1100)} = Max (0, – 300) = 0

So, the payoff from the OTM Call Option = Premium received – Premium paid = 0 – 30 = – Rs. 30

Leg 3: Premium received on the two ATM Call Options of strike price Rs. 1000 = 2*80 = Rs. 160

Premium paid on the two ATM Call Options of strike price Rs. 1000 = 2* Max {0, (Spot price –  Strike price)} = 2* Max {0, (800 – 1000)} = 2*Max (0, – 200) = 0

So, the payoff from the two ATM Call Options = Premium received – Premium paid = 160 – 0 = Rs. 160

Net payoff = Payoff from ITM Call Option + Payoff from OTM Call Option + Payoff from two ATM Call Options = (– 140) + (– 30) + 160 = – Rs. 10

If the stock closes at Rs. 1090 on expiry: Leg 1 and leg 3 expires ITM, while leg 2 expires OTM

Leg 1: Premium paid on the ITM Call Option of strike price Rs. 900 = Rs. 140

Premium received on the ITM Call Option of strike price Rs. 900 at expiry = Max {0, (Spot price – Strike price)} = Max {0, (1090 – 900)} = Max (0, 190) = Rs. 190

So, payoff from the ITM Call Option = Premium received – Premium paid = 190 – 140 = Rs. 50

Leg 2: Premium paid on the OTM Call Option of strike price Rs. 1100 = Rs. 30

Premium received on OTM Call Option of strike price Rs. 1100 at expiry = Max {0, (Spot price – Strike price)} = Max {0, (1090 – 1100)} = Max (0, – 10) = 0

So, payoff from the OTM Call Option = Premium received – Premium paid = 0 – 30 = – Rs. 30

Leg 3: Premium received on the two ATM Call Options of strike price Rs. 1000 = 2*80 = Rs. 160

Premium paid on the two ATM Call Options of strike price Rs. 1000 = 2* Max {0, (Spot price –  Strike price)} = 2* Max {0, (1090 – 1000)} = 2*Max (0, 90) = 2* 90 = Rs. 180

So, the payoff from the two ATM Call Options = Premium received – Premium paid = 160 – 180 = – Rs. 20

Net Payoff = Payoff from ITM Call Option + Payoff from OTM Call Option + Payoff from two ATM Call Options = 50 + (– 30) + (– 20) = 0

If the stock closes at Rs. 1200 on expiry: All the three legs expire ITM

Leg 1: Premium paid on the ITM Call Option of strike price Rs. 900 = Rs. 140

Premium received on the ITM Call Option of strike price Rs. 900 at expiry = Max {0, (Spot price – Strike price)} = Max {0, (1200 – 900)} = Max (0, 300) = Rs. 300

So, the payoff from the ITM Call Option = Premium received – Premium paid = 300 – 140 = Rs. 160

Leg 2: Premium paid on the OTM Call Option of strike price Rs.1100 = Rs. 30

Premium received on the OTM Call Option of strike price Rs. 1100 at expiry = Max {0, (Spot price – strike price)} = Max {0, (1200 – 1100)} = Max (0, 100) = Rs. 100

So, the payoff from the OTM Call Option = Premium received – Premium paid = 100 – 30 = Rs. 70

Leg 3: Premium received on the two ATM Call Options of strike price Rs. 1000 = 2*80 = Rs. 160

Premium paid on the two ATM Call Options of strike price Rs. 1000 = 2* Max {0, (Spot price –  Strike price)} = 2* Max {0, (1200 – 1000)} = 2*Max (0, 200) = 2*200 = Rs. 400

So, the payoff from the two ATM Call Options = Premium received – Premium paid = 160 – 400 = – Rs. 240

Net payoff = Payoff from ITM Call Option + Payoff from OTM Call Option + Payoff from two ATM Call Options = 160 + 70 + (– 240) = – Rs. 10

Additional Read: Chapter 4: Options Trading – Long Call (Call Buyer)

Summary

• A Long Call Butterfly is a multi-leg Options strategy that can be used when one has a neutral market outlook.
• A Long Call Butterfly strategy involves selling two ATM Call Options and simultaneously purchasing one ITM Call Option and one OTM Call Option where the three strike prices have an equal difference.
  • Breakeven: Since there are three trades involved, there are two breakeven points:
    • 1. Upper breakeven point = Strike price of OTM Call Option – (Premium of ITM Call Option + Premium of OTM Call Option – 2*Premium of ATM Call Options)
    • 2. Lower breakeven point = Strike price of ITM Call Option + (Premium of ITM Call Option + Premium of OTM Call Option – 2*premium of ATM Call Options)
• Maximum profit: Difference between adjacent strike prices – Net premium paid
• Maximum risk: Limited to the net premium paid i.e. (Premium of ITM Call Option + Premium of OTM Call Option – 2*Premium of ATM Call Option)

In the next chapter, we will look at one more neutral-view Options strategy: The Short Straddle. 

Disclaimer:

ICICI Securities Ltd. ( I-Sec). Registered office of I-Sec is at ICICI Securities Ltd. - ICICI Venture House, Appasaheb Marathe Marg, Prabhadevi, Mumbai - 400 025, India, Tel No : 022 - 2288 2460, 022 - 2288 2470. The contents herein above shall not be considered as an invitation or persuasion to trade or invest.  I-Sec and affiliates accept no liabilities for any loss or damage of any kind arising out of any actions taken in reliance thereon. The contents herein above are solely for informational purpose and may not be used or considered as an offer document or solicitation of offer to buy or sell or subscribe for securities or other financial instruments or any other product. Investments in securities market are subject to market risks, read all the related documents carefully before investing. The contents herein mentioned are solely for informational and educational purpose.